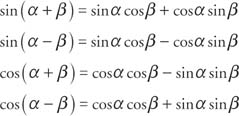Addition Identities

Let us study about Addition Identities,
The fundamental (basic) identities discussed in the previous section involved only one variable. The following identities, involving two variables, are called trigonometric addition identities.These four identities are sometimes called the sum identity for sine, the difference identity for sine, the sum identity for cosine, and the difference identity for cosine, respectively. The verification of these four identities follows from the basic identities and the distance formula between points in the rectangular coordinate system. Explanations for each step of the proof will be given only for the first few examples that follow.

Example 1: Change sin 80° cos 130° + cos 80° sin 130° into a trigonometric function in one variable (Figure 1 ).

Figure 1

Drawing for Example 1.

Additional identities can be derived from the sum and difference identities for cosine and sine.

Hope the above explanation helped you..

Introduction of Argand plane

Let me explain about Argand plane,

ARGAND PLANE :

A complex number z = x + iy written as ordered pair (x, y) can be represented by a point P whose Cartesian coordinates are (x, y) referred to axes OX and OY, usually called the real and the imaginary axes. The plane of OX and OY is called the Argand diagram or the complex plane.



MODULUS OF A COMPLEX NUMBER

Let z = x + iy be a complex number then its magnitude is defined by the real number √x2+y2 and is denoted by |z|.


ARGUMENT OF A COMPLEX NUMBER :

If z = x + iy then angle θ given by tan θ = y/x is said to be the argument or amplitude of the complex number z and is denoted by arg (z) or amp (z). In case of x = 0 (where y ≠ 0), arg (z) = + π/2 or –π/2 depending upon y > 0 or y < y =" 0"> 0 or x < 0 and the complex number is called purely real. The argument of the complex number 0 is not defined.


We can define the argument of a complex number also as any value of the q which satisfies the system of equations cosθ = x√x2+y2, sinθ = y√x2+y2

Hope my explanation was helpful.

Complex number modulus

Let us study about complex number modulus,
Modulus of a complex number is the distance of the complex number from the origin in a complex plane. The modulus | Z | of a complex number Z = x + iy is given by
Modulus is also called as Absolute Value.

Modulus of a complex number Z is also denoted as mod Z.
Modulus| Z | of a complex number Z is also given aswhere is the conjugate complex of Z.


Example of Modulus of a complex number :

The modulus of complex number 3 + 4i is given as

Hope the above explanation helped you.

Harmonic Progression

Harmonic Progression:


Harmonic Progression (HP):

Definition: In mathematics, a harmonic progression is a progression formed by taking the reciprocals of an arithmetic progression.Equivalently, a sequence is a harmonic progression when each term is the harmonic mean of the neighboring terms.

The general form of the harmonic progression is ,

a , a , a , a .............

1+d 1+2d 1+3d

Example:

10, 10/6 , 10/11 , 10/16....

Here a = 10 and d = 5.


A sequence of numbers is said to form a harmonic progression if their reciprocals form an arithmetic progression.
Note:

i) The series formed by the reciprocals of the terms of a geometric series is also a geometric series.
ii) There is no general method of finding the sum of a harmonic progression.
To find the nth term of an H.P

To find the nth term of an H.P, find the nth term of the corresponding A.P. obtained by the reciprocals of the terms of the given H.P. Now the reciprocal of the nth term of an A.P. will be the nth term of the H.P.


There are three types of Progression in math,

*

Arithmetic progression
*

Geometric progression
* Harmonic progression

Hope you like the above example of Harmonic Progression.Please leave your comment if you have any doubts.

Mean

Mean:



Mean:

Introduction:

Mean, median and mode are more common terms in statistics.

The average or mean is calculated by arranging the values from the set in a particular way and computing a single number as being the average of the set.

The median of a list of number can be arranging all the values from lowest value to highest value and select the middle one.

Mode is also a compute of central tendency. In a set of individual observations, the value occurs most time is called as mode.

In general Arithmetic mean (A.M) or average of n number of data x1, x2, …, xn is defined to be the number x such that the sum of the deviations of the observations from x is 0. That is, the arithmetic mean x of n observations x1, x2, …, xn is given by the equation

(x1 − x) +(x2 − x) + ... +(xn − x) = 0

Hence [barx] = x1+x2+x3+…….xn / n

Mean or average= sum of elements / total number of elements

Example: To find the mean or average of 7, 5, 6

Step 1: Find the sum of numbers

7+5+6= 18

Step 2: Calculate the total value. Therefore 3 values

Step 3: Calculate mean use formula 18/3=6

Answer: 6

Hope you like the above example of Mean.Please leave your comments, if you have any doubts.

Percentage:

Percentage:



Percentage:

The word 'percent' is abbreviated from the Latin word 'per-centum' meaning 'per hundred', or 'hundred' or 'hundredth'. The symbol to denote percent is %. This shows the value given is expressed in terms of hundred. Percentage means out of hundred.Percentages are used to express how large/small one quantity is, relative to another quantity. The first quantity usually represents a part of, or a change in, the second quantity, which should be greater than zero. For example, an increase of $ 0.15 on a price of $ 2.50 is an increase by a fraction of 0.15 / 2.50 = 0.06. Expressed as a percentage, this is therefore a 6% increase.

Examples of Percentages:


1. What is 200% of 30?

Answer: 200% × 30 = (200 / 100) × 30 = 60.

2. What is 13% of 98?

Answer: 13% × 98 = (13 / 100) × 98 = 12.74.

3. 60% of all university students are male. There are 2400 male students. How many students are in the university?

Answer: 2400 = 60% × X, therefore X = (2400 / (60 / 100)) = 4000.

1. There are 300 cats in the village, and 75 of them are black. What is the percentage of black cats in that village?

Answer: 75 = X% × 300 = (X / 100) × 300, so X = (75 / 300) × 100 = 25, and therefore X% = 25%.

2. The number of students at the university increased to 4620, compared to last year's 4125, an absolute increase of 495 students. What is the percentual increase?

Answer: 495 = X% × 4125 = (X / 100) × 4125, so X = (495 / 4125) × 100 = 12, and therefore X% = 1


Introduction on percentage increase and decrease:

Percentage is expressing any number in a fraction with the denominator as 100. The symbol used for the percentage is ‘%’. Percentage difference is defined as the comparing a previous value to the new value.

Formula for percentage increase/ decrease = [change in value / old value] * 100
What is the percentage increase from 50 to 54.5?

Example 1 on percent increase and decrease:

Solution:

Change in value = 54.5-50 = 4.5

Percentage increase = [4.5/50] *100

= 0.09*100

= 9%

Hope you like the above example of Percentage.Please leave your comments if you have any doubts.

Linear Equations:

Linear Equations:

Linear Equations:
Definition:A linear equation is defined as an algebraic equation in which every expression is either a stable (constant) or the product of a stable and a single variable. Linear equations can have one or more than one variables. It’s happening with great reliability in applied mathematics. A linear function is one whose diagram (graph) is a straight line.
Linear equations represent a straight line and it may be inclined or horizontal. The general format for a linear equation is as follows,

y = mx +b
where,
m = slope of the line (it is a number).

Functions of Linear Equations:
A mathematical functions is an equation which assigns a single answer to each possible question. A variable denotes an unknown value in the functions and equation.
Example for functions:

The set of all elements in functions and ordered pairs is known as domain; the set of all second elements are called range.

Example:

Functions f(x) = {(1 , 2), (3 , 4), (5 , 6), (7 , 8)}

Here Domain = { 1, 3, 5, 7 } and

Range = { 2, 4, 6, 8 }


Let us now look at few examples of Linear Equations:


Example (1)

-3/4 (16y -12) = 2/3 (18 - 9y)

1/4 (16y x -3 -12 x -3) = 1/3 (18 x 2 - 9y x 2) [Using the distributive property multiplying both the sides with their numerator]

1/4 (-48y + 36) = 1/3 (36 - 18y)

3(-48y+36) = 4(36 - 18y) [Cross multiplication ]

-144y + 108 = 144 - 72y

-144y + 72y = 144 - 108 [ Taking like terms to one side]

-72y = 36

-y = 36/72

y = -1/2 Answer


Hope you liked the example of Linear Equations,Please leave your comment if you have any doubt.